The short answer is: yes!

The hyperbolic tangent (tanh) and logistic sigmoid ($\sigma$) functions are defined as follows:

\[\tanh(z) = \frac{e^x - e^{-x}}{e^x + e^{-x}}, \quad \sigma(x) = \frac{1}{1+e^{-x}}.\]

And if we’d plot those functions side-by-side, the relationship can almost be picked out by eye:

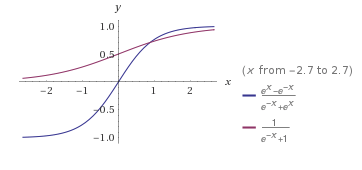
../../images/faq/tanh-sigmoid-relationship/tanh-sigmoid.png

Since the logistic sigmoid function is symmetric around the origin and returns a value in range [0, 1], we can write the following relationship:

\[1 - \sigma(x) = \sigma(-x),\]

I.e.,

\[1 - \frac{1}{1+e^{-x}} = \frac{1}{1+e^{x}}.\]

Now, to see the relationship between tanh and $\sigma$, let’s rearrange the tanh function into a similar form by:

\[\begin{align} \tanh(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}} \\\\ &= \frac{e^x + e^{-x} - 2e^{-x}}{e^x + e^{-x}} \\\\ &= 1 + \frac{-2e^{-x}}{e^x + e^{-x}} \\\\ &= 1 - \frac{2}{e^{2x}+ 1} \end{align}\]

Now, from the logistic sigmoid’s perspective, we have:

\[\begin{align} \tanh(x) = 1 - \frac{2}{e^{2x}+ 1} &= 1 - 2\sigma(-2x) \\ &= 1 - 2 (1 - \sigma(2x)) \\ &= 1 - 2 + 2\sigma(2x) \\ &= 2 \sigma(2x) -1 \\ \end{align}\]

Hence, we can conclude that the tanh function is just a rescaled version of the logistic sigmoid function.



If you like this content and you are looking for similar, more polished Q & A’s, check out my new book Machine Learning Q and AI.