A necessary criterion for the derivative to exist is that a given function is continuous. Does the Rectified Linear Unit (ReLU) function meet this criterion? To address this question, let us look at the mathematical definition of the ReLU function:

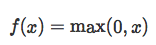
or expressed as a piece-wise defined function:

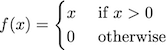
Since f(0)=0 for both the top and bottom part of the previous equation, the ReLU function, we can clearly see that the function is continuous. And if this isn’t immediately obvious, a plot of the ReLU function should make this really clear:

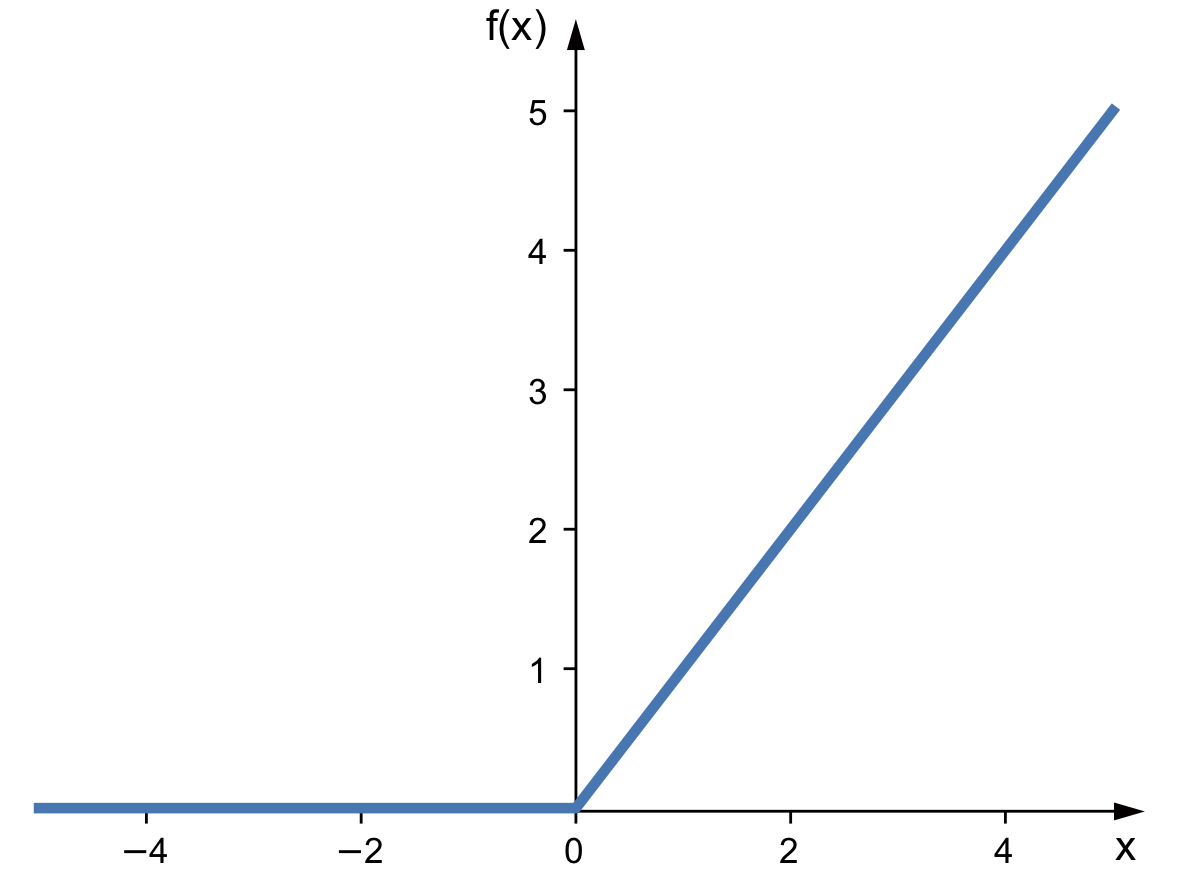
Note that the fact that all differentiable functions are continuous does not imply that every continuous function is differentiable.

The reason why the derivative of the ReLU function is not defined at x=0 is that, in colloquial terms, the function is not “smooth” at x=0.

More concretely, for a function to be differentiable at a given point, the limit must exist. And for the limit to exist, the following 3 criteria must be met:

  1. the left-hand limit exists
  2. the right-hand limit exists
  3. the left-hand and right-hand limits are equal

Before we work through this list, remember, to obtain a derivative of a function f(x) using the fundamental concepts of a derivative, we use the following equation:

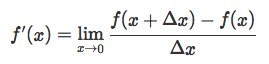
where Δx is an infinitely small, “almost zero” number. This is basically also known as “rise over run” (i.e., how much the output of a function varies with a tiny change of its input).

We can use it to compute the derivative of the ReLU function at x != 0 by just substituting in the max(0, x) expression for f(x):

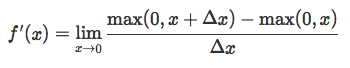
Then, we obtain the derivative for x > 0,

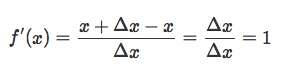
and for x < 0,

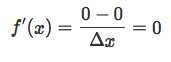
Now, to understand why the derivative at zero does not exist (i.e., f’(0)=DNE), we need to look at left- and right-handed limit. That is, let’s approach “0” from the left-hand side (i.e., think of Δx as an infinitely small negative number, and then subsitute it into the earlier equation):

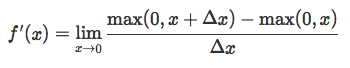
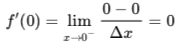
Then we can do the same thing with the right-handed limit:

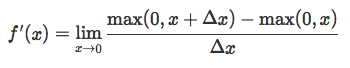
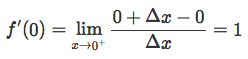
As we can see, the left-hand limit and the right-hand limit are not equal, and there is no single derivative at x=0; hence, we say that the derivative f’(x=0) is not defined or does not exist (DNE):

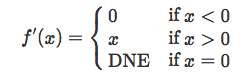
In practice, it’s relatively rare to have x=0 in the context of deep learning, hence, we usually don’t have to worry too much about the ReLU derivative at x=0. Typically, we set it either to 0, 1, or 0.5.



If you like this content and you are looking for similar, more polished Q & A’s, check out my new book Machine Learning Q and AI.