According to the lottery ticket hypothesis [ref], a randomly initialized neural network can contain a subnetwork that, when trained on its own, can achieve the same accuracy on a test set as the original network after being trained for the same number of steps.

The figure below illustrates the training procedure for the lottery ticket hypothesis in a more visual way. We will go through the steps one by one to help clarify the concept.

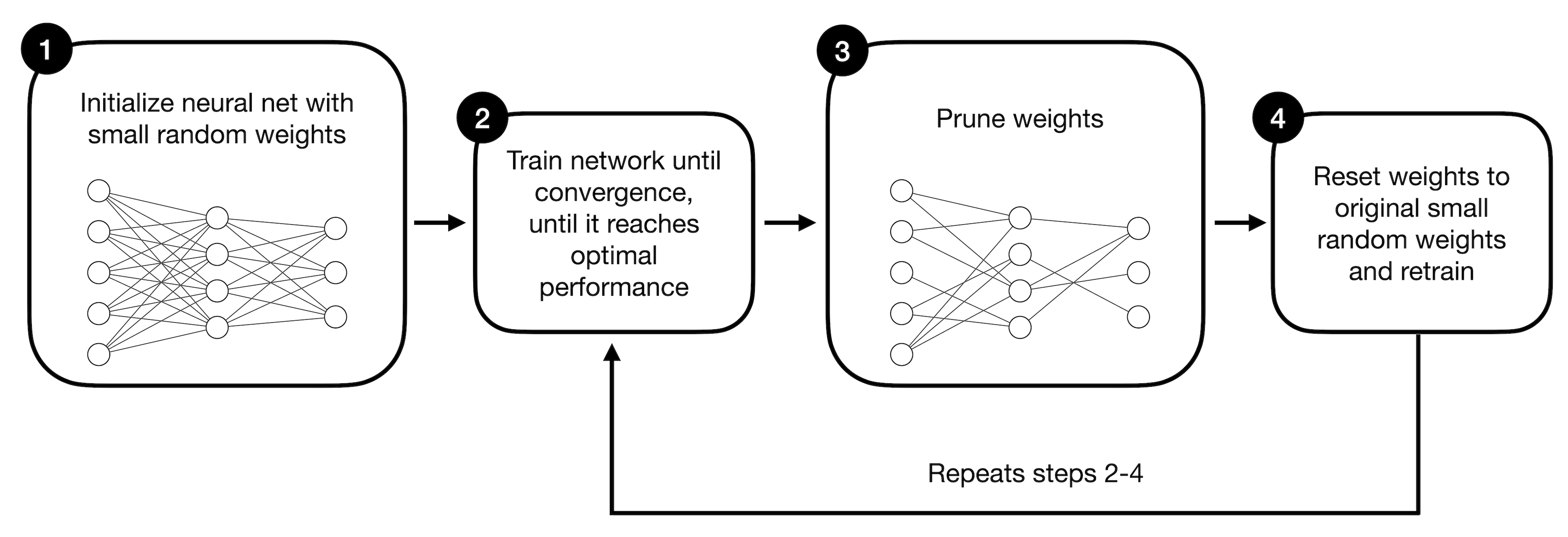
We start with a large neural network (1) that we train until convergence (2), which means that we put in our best efforts to make it perform as best as possible on a target dataset – for example, minimizing training loss and maximizing classification accuracy. This large neural network is initialized as usual using small random weights.

Next, we prune the neural network’s weight parameters (3), removing them from the network. We can do this by setting the weights to zero to create sparse weight matrices. Which weights do we prune? The original lottery hypothesis approach follows a concept known as iterative magnitude pruning, where the weights with the lowest magnitudes are removed in an iterative fashion.

After the pruning step, we reset the weights to the original small random values used in step 1. It’s worth emphasizing that we do not reinitialize the pruned network with any small random weights (as it is typical for iterative magnitude pruning) but reuse the weights from step 1.

The pruning steps 2-4 are then repeated until the desired network size is reached. For example, in the original lottery ticket hypothesis paper, the authors successfully reduced the network to 10% of its original size without sacrificing classification accuracy. As a nice bonus, the pruned (sparse) network, referred to as the winning ticket, even demonstrated improved generalization performance compared to the original (large and dense) network.



This is an abbreviated answer and excerpt from my book Machine Learning Q and AI, which contains a more verbose version with additional illustrations.