Yes, you can replace a fully connected layer in a convolutional neural network by convoplutional layers and can even get the exact same behavior or outputs. There are two ways to do this: 1) choosing a convolutional kernel that has the same size as the input feature map or 2) using 1x1 convolutions with multiple channels.

To illustrate and demonstrate this, assume we have a 2x2 input image:

import torch
inputs = torch.tensor([[[[1., 2.],
                         [3., 4.]]]])

inputs.shape

torch.Size([1, 1, 2, 2])

Fully Connected Layers

A fully connected layer, which maps the 4 input features two 2 outputs, would be computed as follows:

fc = torch.nn.Linear(4, 2)

weights = torch.tensor([[1.1, 1.2, 1.3, 1.4],
                        [1.5, 1.6, 1.7, 1.8]])
bias = torch.tensor([1.9, 2.0])
fc.weight.data = weights
fc.bias.data = bias

torch.relu(fc(inputs.view(-1, 4)))

tensor([[14.9000, 19.0000]], grad_fn=<ReluBackward0>)

Method 1: Convolutions with kernels equal to the input size

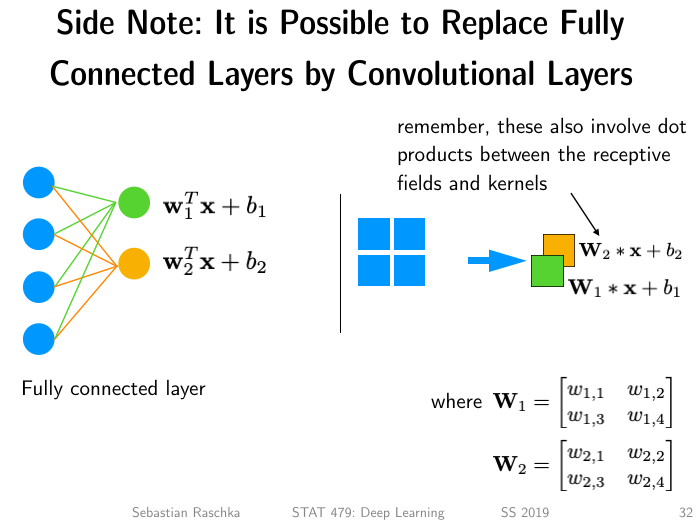
We can obtain the same outputs if we use convolutional layers where the kernel size is the same size as the input feature array:

conv = torch.nn.Conv2d(in_channels=1,
                       out_channels=2,
                       kernel_size=inputs.squeeze(dim=(0)).squeeze(dim=(0)).size())
print(conv.weight.size())
print(conv.bias.size())

torch.Size([2, 1, 2, 2])
torch.Size([2])

conv.weight.data = weights.view(2, 1, 2, 2)
conv.bias.data = bias

torch.relu(conv(inputs))

tensor([[[[14.9000]],

         [[19.0000]]]], grad_fn=<ReluBackward0>)

Methods 2: Convolution with 1x1 kernels

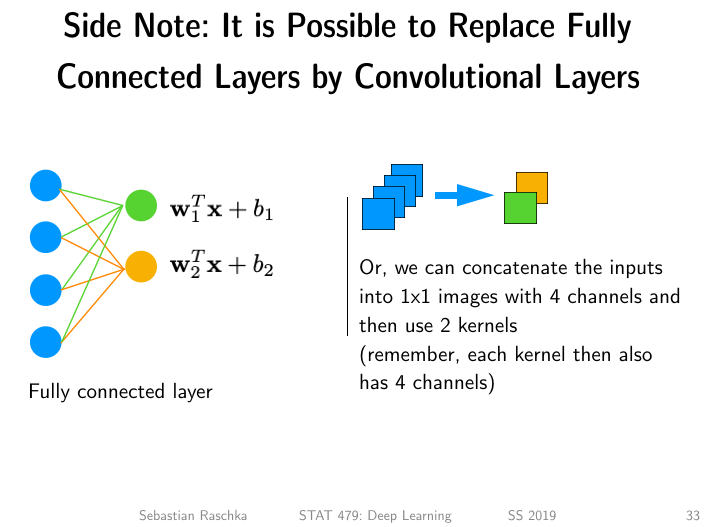
Similarly, we can replace the fully connected layer using a convolutional layer when we reshape the input image into a num_inputs x 1 x 1 image:

conv = torch.nn.Conv2d(in_channels=4,
                       out_channels=2,
                       kernel_size=(1, 1))

conv.weight.data = weights.view(2, 4, 1, 1)
conv.bias.data = bias
torch.relu(conv(inputs.view(1, 4, 1, 1)))

tensor([[[[14.9000]],

         [[19.0000]]]], grad_fn=<ReluBackward0>)



If you like this content and you are looking for similar, more polished Q & A’s, check out my new book Machine Learning Q and AI.