Since there are so many different approaches, let’s break it down to “feature selection” and “feature extraction.”

Some examples of feature selection:

  • L1 regularization (e.g., Logistic regression) and sparsity
  • variance thresholds
  • recursive feature elimination based on the weights of linear models
  • random forests / extra trees and feature importance (calculated as average information gain)
  • sequential forward/backward selection
  • genetic algorithms
  • exhaustive search

Some examples of feature extraction:

  • Principal Component Analysis (PCA), unsupervised, returns axes of maximal variance given the constraint that those axes are orthogonal to each other
  • Linear Discriminant Analysis (LDA; not to be confused with Latent Dirichlett Allocation), supervised, returns axes that maximizes class separability (same constraint that axes are also orthogonal); and another article: Linear Discriminant Analysis bit by bit
  • kernel PCA: uses kernel trick to transform non-linear data to a feature space were samples may be linearly separable (in contrast, LDA and PCA are linear transformation techniques
  • supervised PCA
  • and many more non-linear transformation techniques, which you can find nicely summarized here: Nonlinear dimensionality reduction

** So, which technique should we use? **

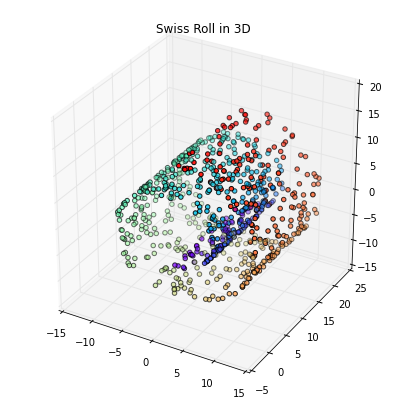
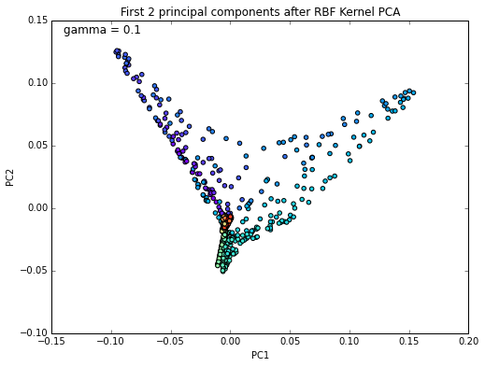
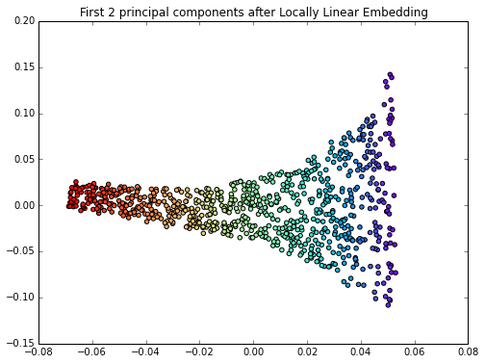
This also follows the “No Lunch Theorem” principle in some sense: there is no method that is always superior; it depends on your dataset. Intuitively, LDA would make more sense than PCA if you have a linear classification task, but empirical studies showed that it is not always the case. Although kernel PCA can separate concentric circles, it fails to unfold the Swiss Rroll, for example; here, locally linear embedding (LLE) would be more appropriate.



If you like this content and you are looking for similar, more polished Q & A’s, check out my new book Machine Learning Q and AI.